LSM 树介绍和优化

这篇文章的设计思路来源于此: B 站视频

不同于 B+ 树适用于读多写少的场景, LSM 树更适合用于写多读少的场景. 像是 LevelDB 和 RocksDB 都是基于 LSM 树创建的. 整篇文章的大致思路如图所示.

LSM 树的构建思路推演

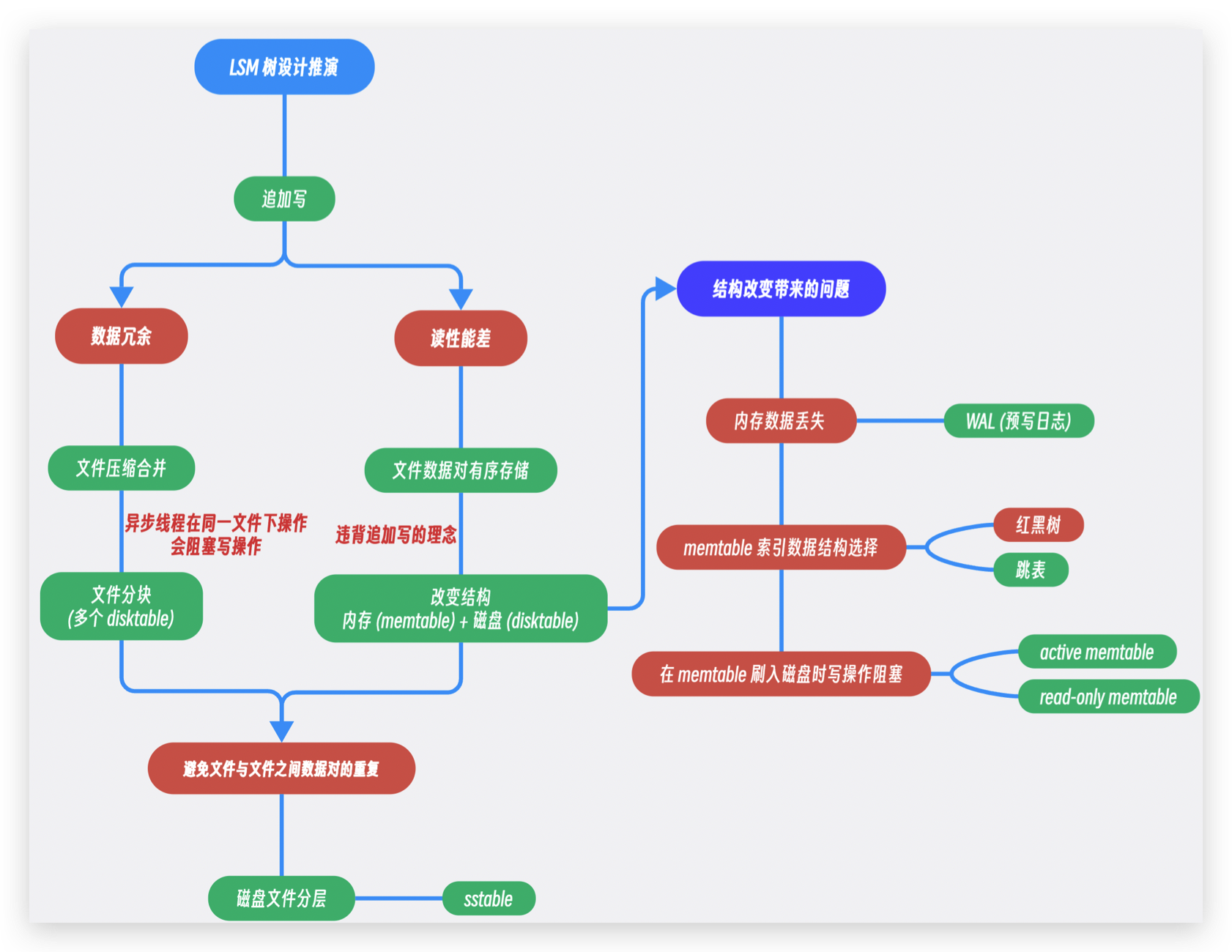
就地写 v.s. 追加写

LSM 树是基于追加写操作开始构建的. 我们首先可以看看追加写和就地写之间的区别

• 就地写: 首先在文件中找出需要修改的数据对的位置 (也就是查询数据对), 然后直接对原有的数据进行覆盖; 这一过程涉及到磁盘的随机 IO, 我们知道磁盘的 IO = 磁盘的寻道时间 + 磁头的旋转时间 + 数据读取/写入时间, 随机 IO 带来的性能开销过于庞大, 所以在写操作较多的场景下使用就地写并不划算
• 追加写: 直接在文件的末端添加数据, 追加写使用了磁盘的顺序 IO, 相比于随机 IO, 顺序 IO 花在寻道时间和刺头的旋转时间可以忽略不计.

追加写使用了磁盘的顺序 IO, 因此拥有比就地写操作更好的性能, 但是追加写同时也带来了两点困扰.

• 追加写会造成数据冗余; 也就是一个数据对可能会存在多个版本, 这些旧的版本除了挤占文件空间之外毫无用处.
• 在追加写机制下的读操作性能比较差且不稳定 (O(N)), 一个数据对的读取需要从磁盘文件末尾倒序查找, 数据对有可能在中途找到, 但是也有可能不存在于文件中, 这个时候就需要遍历整个文件.

对于数据冗余的优化

文件合并压缩: 使用异步线程清除重复数据对

LSM 在构建的过程中分别对这两个缺陷进行了优化. 首先是对于文件的数据冗余, 我们可以启动一个异步线程定期清理文件的重复数据对. 但是在只有一个文件的情况下, 异步线程容易与执行读写操作的主线程产生冲突, 线程的互斥机制会使得写操作在异步线程执行的时候保持阻塞.

文件分块: 分成多个 disktable 文件

为了避免写操作被阻塞, 我们可以把一整个存储数据对的文件分成一个一个的小文件 (disktable), 写操作只会执行在最新的 disktable, 当一个 disktable 的大小达到一个阈值之后, 新的 disktable 文件就会被创建, 这个时候旧文件就可以由异步线程清理重复数据. 文件分块避免了异步清理线程和执行读写操作的主线程之间的冲突, 从而使得追加写的效率最大化. 但是在文件分块的机制下, 读操作性能还是没有得到优化, 此时的读操作仍然需要遍历每一个 disktable 文件来找出需要读取的数据对.

对于读性能差的优化

对于如何优化读操作, 首先可以使得每一个 disktable 文件中的数据对有序存储, 这样子可以利用索引来降低检索的时间复杂度; 但是文件数据的有序存储在一定程度上跟追加写的理念相违背. 为了解决这个问题, 我们可以将存储结构优化更改为位于内存中的 memtable 以及位于磁盘中的 disktable.

结构更改 1: 内存文件 (memtable) + 磁盘文件 (disktable)

在内存中创建执行写操作的文件 (memtable), memtable 作为写操作的唯一入口包含以下特性:

• memtable 可以按照顺序来存储数据对
• memtable 内不会有重复的数据对
• memtable 在内存中采用就地写
• memtable 的大小在达到一定的阈值之后会被刷入 (flush) 磁盘, 成为 disktable

memtable 的特性可以使得读操作的性能提升, 于此同时写操作的性能也没有受到很大的影响 原因如下:

• 虽然 memtable 的写操作是就地写, 但是我们知道内存的访问大概是 100 - 300 个 CPU 时钟周期 (大概估算就是微妙级别(us)), 而磁盘的访问因为涉及到磁头移动 (寻道时间 + 旋转时间), 大概估算就是毫秒级别. 所以内存的随机 IO 相比于磁盘 IO 性能花销要小很多, 所以不会对写操作有很大的性能损耗.
• 由于 memtable 是按照顺序来存储数据对的, 我们可以使用二分查找的方式来减少读操作的查询时间 (O(N) -> O(log N))
• 就算查询的数据对不存在于 memtable, 读操作在 disktable 的查询也是 O(log N) 时间复杂度的. 这是因为 disktable 在本质上就是大小达到阈值的 memtable. 所以每一个 disktable 的数据对都是有序存储且没有重复数据对的.

但是内存文件的引入也带来了几个问题:

• memtable 文件的数据在内存中是有可能因为机器宕机的缘故丢失的, 我们应该如何防止内存中的数据丢失?
• memtable 文件大小在达到阈值之后会被刷入磁盘中, 但是文件刷入过程中产生的写操作需要保持阻塞, 我们应该如何避免写操作阻塞?
• 我们应该选择什么数据结构来有序存储 memtable 中的数据对?

如何解决结构更改带来的问题?

使用预写日志 (Write Ahead Logging, WAL) 来防止内存中的数据丢失

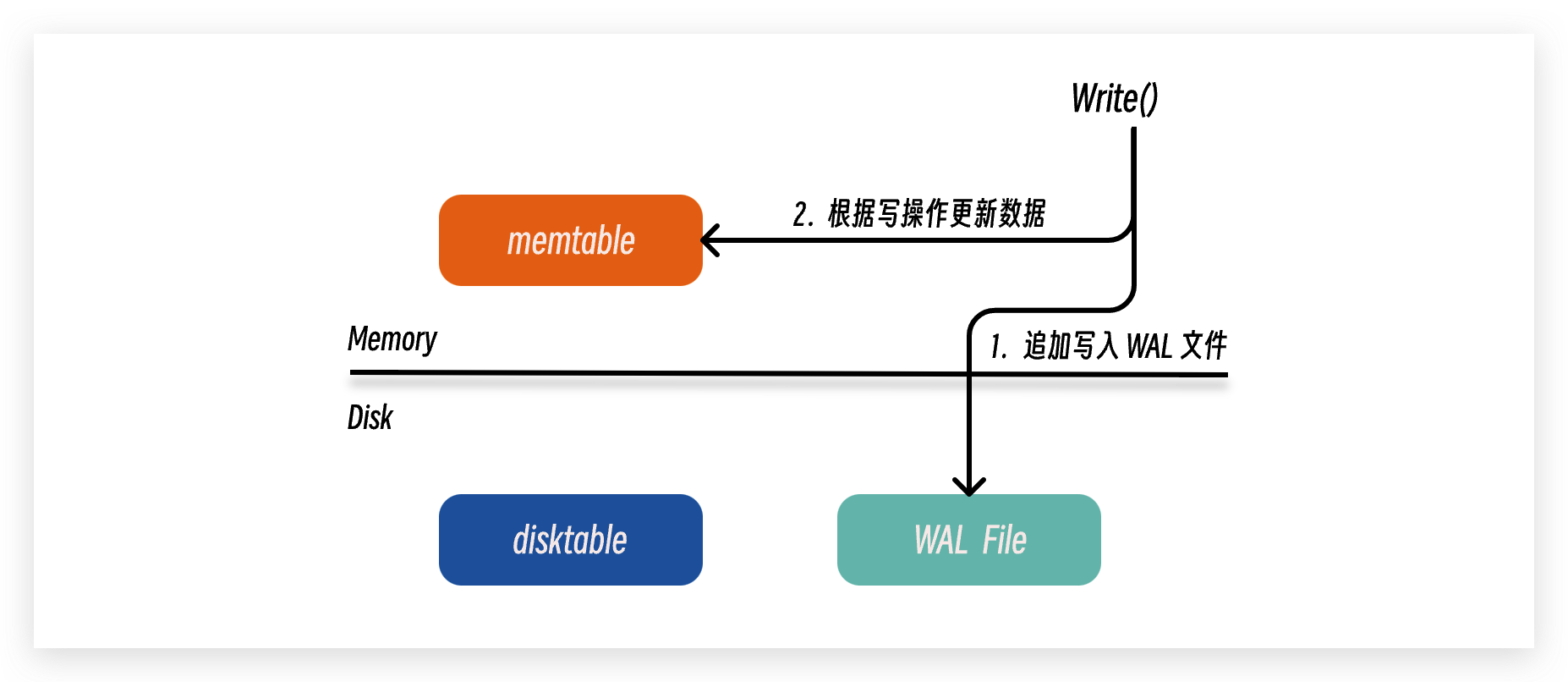
在处理来自客户端的写操作的时候, 我们可以先以追加写的形式将写操作指令写入磁盘中的 WAL 文件, 然后再对内存中的 memtable 进行数据的更新, 等到数据更新完毕之后再返回响应给客户端; 这样子即使内存中的数据丢失, 我们也可以通过重新执行 WAL 文件中的操作指令来恢复 memtable 的数据.

虽然 WAL 文件位于磁盘空间, 但是操作指令数据是以追加写 (磁盘顺序 IO) 的方式存入 WAL 文件中的, 所以 WAL 文件不会成为性能瓶颈. 除此之外, 当一个 memtable 达到阈值被刷入磁盘完成持久化之后, 我们就可以放心删掉原来的 WAL 文件; 因此我们可以一直保持用一个 WAL 文件来持久化操作指令, 同时 WAL 文件的大小也在可控范围之内.

使用 active memtable + read-only memtable 的形式来防止写操作阻塞

当 memtable 的文件大小达到阈值之后, 我们可以将其标记为 read-only, 然后创建一个新的 active memtable; 这样子在 read-only memtable 刷入磁盘的时候, 写操作的数据更新可以存储在 active memtable 中, 避免被阻塞.

使用跳表作为 memtable 内的数据结构来有序存储数据对

红黑树和跳表都可以有效存储或操作有序数据对 (相关操作的时间复杂度属于同一数量级 - O(log N)), 但是跳表相比于红黑树有两大优势:

• 跳表的实现要比红黑树的实现要简单的多; 红黑树需要在树结点的修改, 插入或者删除的操作中付出额外的维护成本, 以保持红黑树对于平衡性的要求 (任意左右子树的高度差不能超过 2 倍); 而跳表本质上就是一个多层单向有序链表, 实现自然要简单的多.
• 跳表相比于红黑树有着更好的并发性; 红黑树因为需要对树结点进行染色和旋转来维护自身的平衡性, 因此他在每次写操作的时候都需要对整棵树加锁; 但是跳表只需要对写操作涉及到的结点边界范围内加锁就可以了, 因此跳表支持更细的并发锁粒度.

内存 + 磁盘文件结构下的读写操作

在当前的 memtable + disktable 结构下, 写操作造成的数据更新只需要存储在内存中 active memtable 中, 执行效率高; 但是对于读操作, 如果查询的数据对不在内存中, 那么读操作需要根据磁盘文件创建的时间倒序遍历每个磁盘文件, 直到找到对应的数据对或者遍历完所有的磁盘文件为止; 虽然我们可以通过文件内的跳表结构来缩减搜索的时间, 但是因为需要遍历文件的个数多, 读操作的执行效率相比于写操作差上不少, 因此我们需要继续优化磁盘文件的结构. 现有的结构只能做到单个磁盘文件不包含重复数据 (磁盘中的 disktable 从内存中的 memtable 转换过来), 我们需要减少文件与文件之间的重复数据.

磁盘文件分层

磁盘文件分层具有以下性质:

• 所有的磁盘文件会被分成 N + 1 层
• 每一层的磁盘文件个数都一致, 且每一层的磁盘文件的总大小都有一个阈值; 通常来说第 i + 1 层的磁盘文件总大小是第 i 层的 k 倍 (k >= 10)
• 当内存中的 memtable 的大小达到阈值之后, 他就会被刷入磁盘中的第 0 层 (level 0)
• 当第 i 层的磁盘文件总大小达到阈值之后, 数据对从第 i 层到第 i + 1 层的有序归并流程就会被触发.

从以上性质我们可以知道, 数据的流动方向是从上层向下层流动的; 除此之外, 第 0 层的磁盘文件都是从 memtable 转换过来的, 所以第 0 层只能做到单个文件存储有序且不重复的数据对; 但是从第 1 层开始, 我们可以通过向下层文件数据对的有序归并来保证每一层的磁盘文件都全局有序且不包含重复数据对.

有序归并

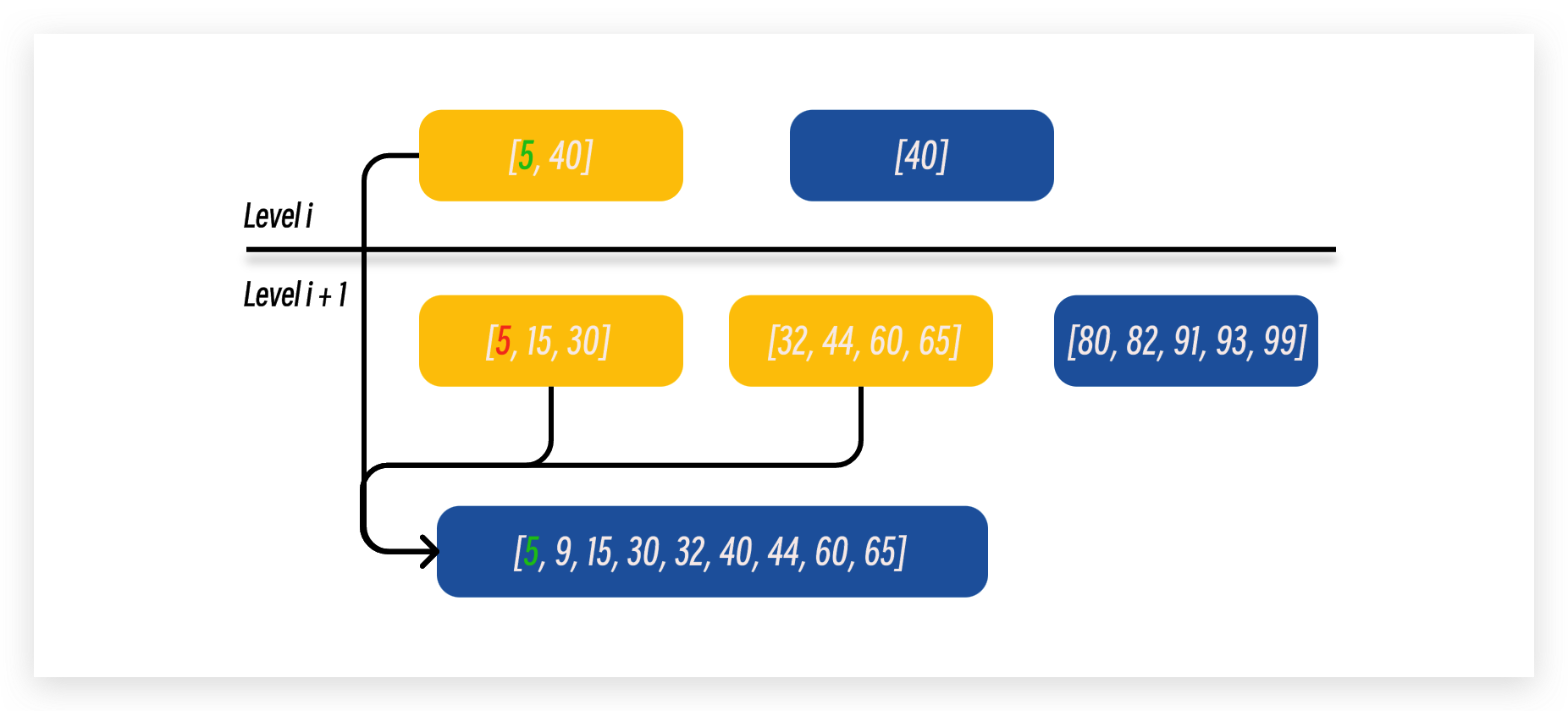
当第 i 层的磁盘文件总大小达到阈值之后, LSM 树会随机选择一个磁盘文件与下层磁盘文件进行归并. 我们可以通过第 i 层磁盘文件的最大最小边界范围来找到第 i + 1 层中存在边界交叉的磁盘文件来进行排序. 以下图为例子, 第 i 层中被选中的文件是 [5, 40], 我们可以通过这个范围找到第 i + 1 层中边界范围有交叉的文件, 也就是 [5, 30] 以及 [32, 65], 然后在进行有序归并.

有序归并的过程也很简单:

• 先在第 i + 1 层创建一个空的磁盘文件
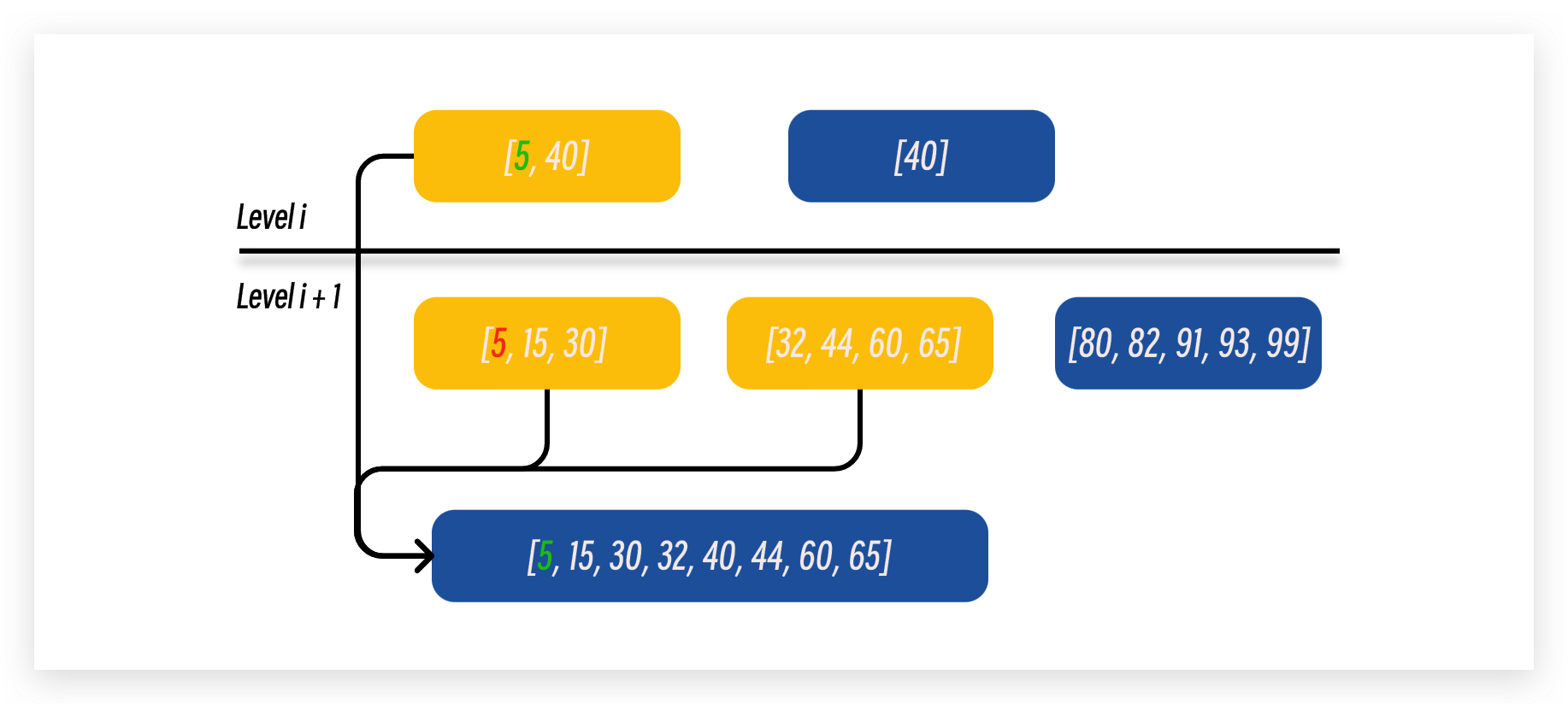
• 然后为每一个需要合并的磁盘文件分配一个指针遍历文件中的数据对. 在下图例子中, 我们只需要对将三个指针指向的数据对的最小值存入新的磁盘文件中, 然后在向前移动对应的指针. 持续这个过程知道所有的指针都遍历完成对应的磁盘文件.
• 对于 key 值同样大小的数据对, 应该选择上层文件中的数据对, 因为 LSM 树结构中数据是从浅层到深层流动的, 所以第 i 层的数据对是最新版本.
• 如果合并之后的磁盘文件容量过大 (文件容量 > 该层文件总容量/该层文件个数), 我们还需要在最后将其做一个拆分.

SSTable (Sorted String Table)

LSM 树为磁盘文件提供了一个 SSTable 的文件格式, 用于优化读操作的数据检索. SSTable 具有一下性质:

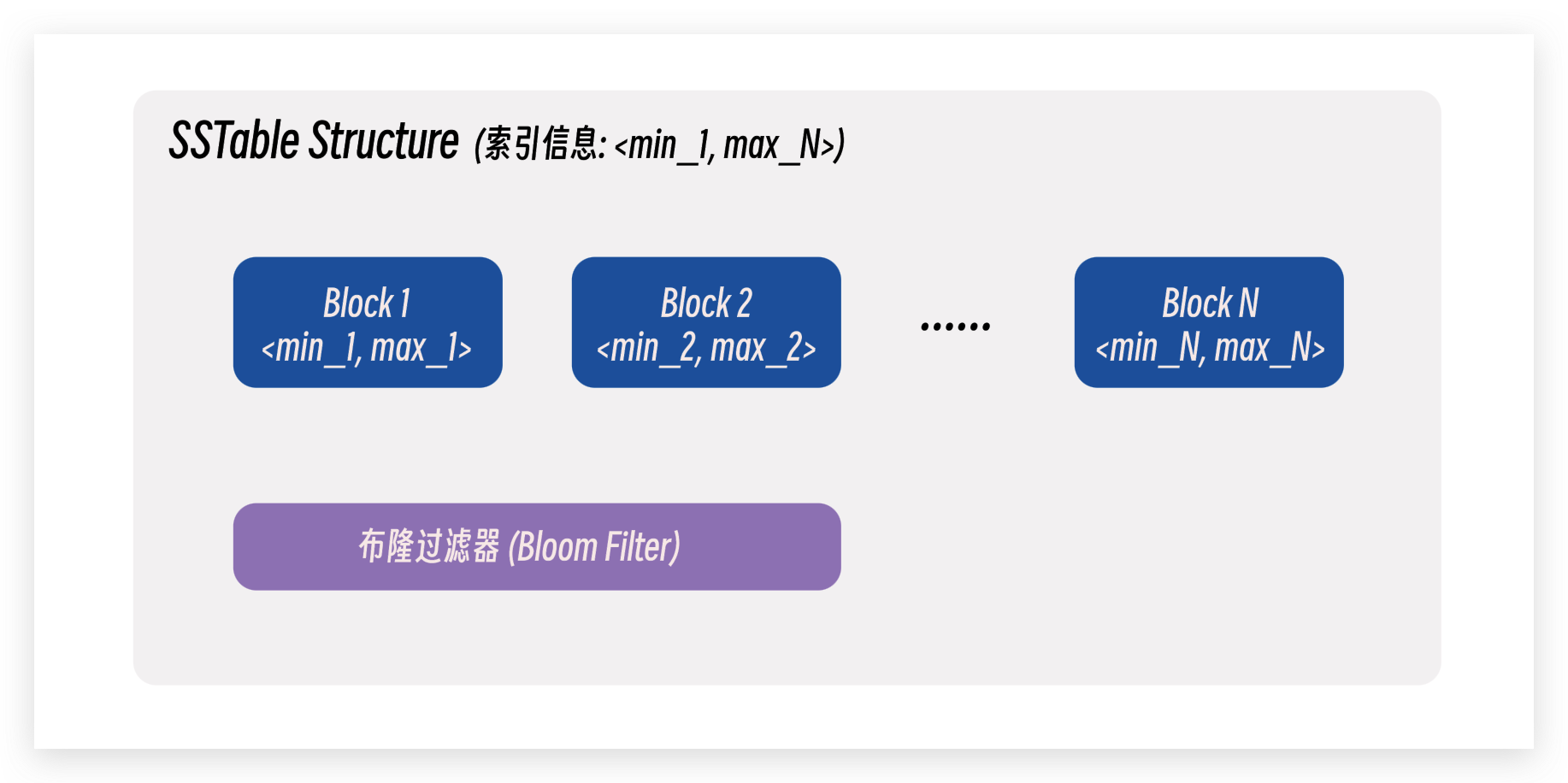
• SSTable 内部会分成多个 blocks, 这些 block 在逻辑意义上属于 SSTable.
• 每一个 block 存储一部分有序且不重复的数据, 同时也存储了数据对 <min, max> 的索引信息, 用于加速检索.
• 除此之外, SSTable 还维护了一个全局的索引信息, 也就是下图中的 <min_1, max_N>.
• 最后, 每一个 SSTable 都会配备一个布隆过滤器 (bloom filter), 用于检测数据是否存在于当前的 SSTable 中.

除此之外, LSM 树也会在每一层维护 SSTable 的索引信息, 也就是这一层中每一个 SSTable 的最大最小数据对信息. 综上所述, LSM 对于读操作的优化流程如下:

• LSM 首先会检测读操作的数据对是否落入这一层的 SSTable 的数据对范围内; 如果不在范围内, 那么就向下一层检索.
• 如果数据对落入该层中的某一个 SSTable 的数据对范围, 那么首先使用布隆过滤器检测数据是否存在于该 SSTable. 因为布隆过滤器有着假阳性的性质, 所以如果布隆过滤器显示数据不存在, 那么就停止该层的检索, 跳转到下一层继续操作. 如果布隆过滤器显示存在, 那么就需要检测这个 SSTable.
• 读操作可以通过 SSTable 中每一个 block 的索引信息 (也就是数据对边界) 来快速定位到对应的 block, 然后利用 block 中的跳表结构进行检索.

通过上述流程, 我们可以略过大部分的数据对检索, 从而提高读操作的效率.

总结

最后我们来对 LSM 树的性质做一个总结:

• LSM 树采用了内存 (memtable) + 磁盘文件分层 (SSTable) 结构存储数据, 其中内存中的 memtable 采用就地写, 而磁盘中的 SSTable 文件采用顺序写.
• 读写操作的入口都是在内存中的 active memtable.
• 写数据的流动方向于读操作的执行方向一致: active memtable -> read-only memtable -> level 0 sstables -> … -> level N sstables, 因此浅层数据属于热数据, 而深层数据属于冷数据.
• 当内存中的 active memtable 的大小达到阈值之后, 他就会被标记为 read-only memtable, 然后被刷入磁盘文件分层结构中的第 0 层.
• 磁盘第 i 层的文件总容量达到阈值之后会启动有序归并流程向第 i + 1 层进行数据归并, 从而保证从第 1 层开始的单层文件数据对唯一且有序的性质.

The End.