Treap

Treap 是一种同时满足 Binary Search Tree (BST) 和 Heap 性质的数据结构 (这篇文章采用 Min-Heap). 也就是说 treap 中的任意一个节点的 key 总是比左子树的任意节点的 key 要大, 也比右子树的任意节点的 key 要小. 与此同时, 这个节点的 priority 要比他子树的任意节点的 priority 要小.

当我们在使用 BST 的时候, 树的平衡往往得不到保证. 最坏的结果就是树的高度为 \(O(n)\). 而一个完美的平衡二叉树的高度正好就是 \(\log n\). 而二叉树的高度往往决定了对树操作的复杂度. Treap 通过保证整棵树所有节点都遵循 Heap 性质来协助二叉树的平衡 (减少树的高度).

Rotation

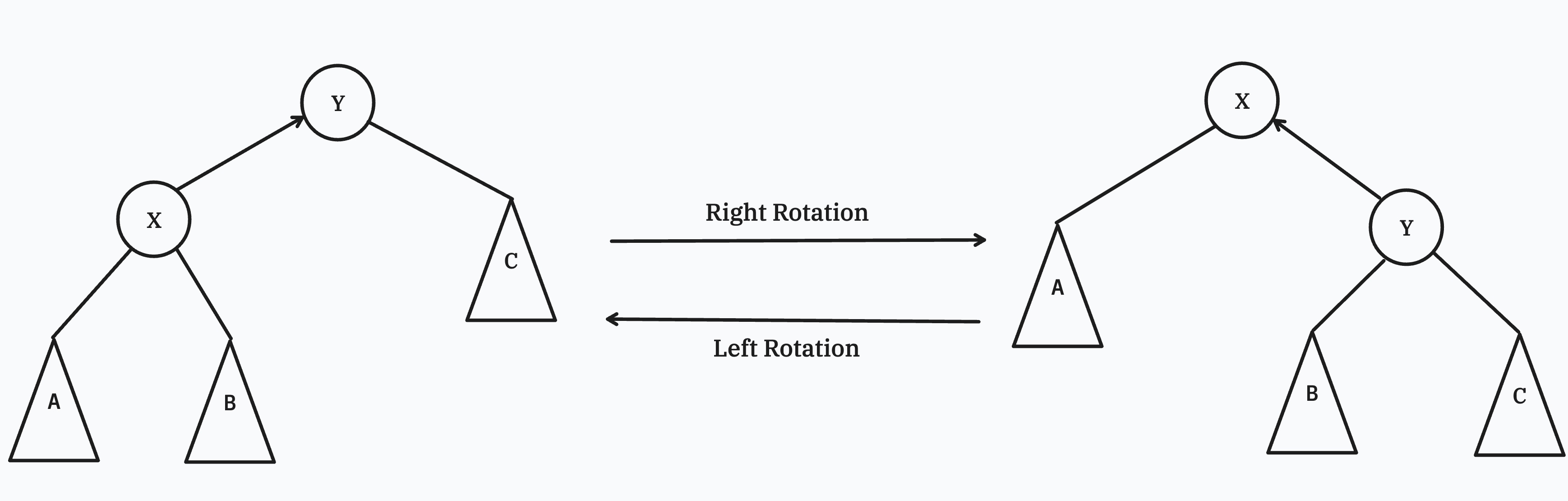
Treap 使用 rotations 来保持 Heap 的性质. 在左旋或者右旋的过程中, BST 的性质会一直被保持.

• 当 node X 的 priority 要比 node Y 的 priority 要小的时候, 需要右旋来保持 Min-Heap 的性质
• 当 node Y 的 priority 要比 node X 的 priority 要小的时候, 需要左旋来保持 Min-Heap 的性质

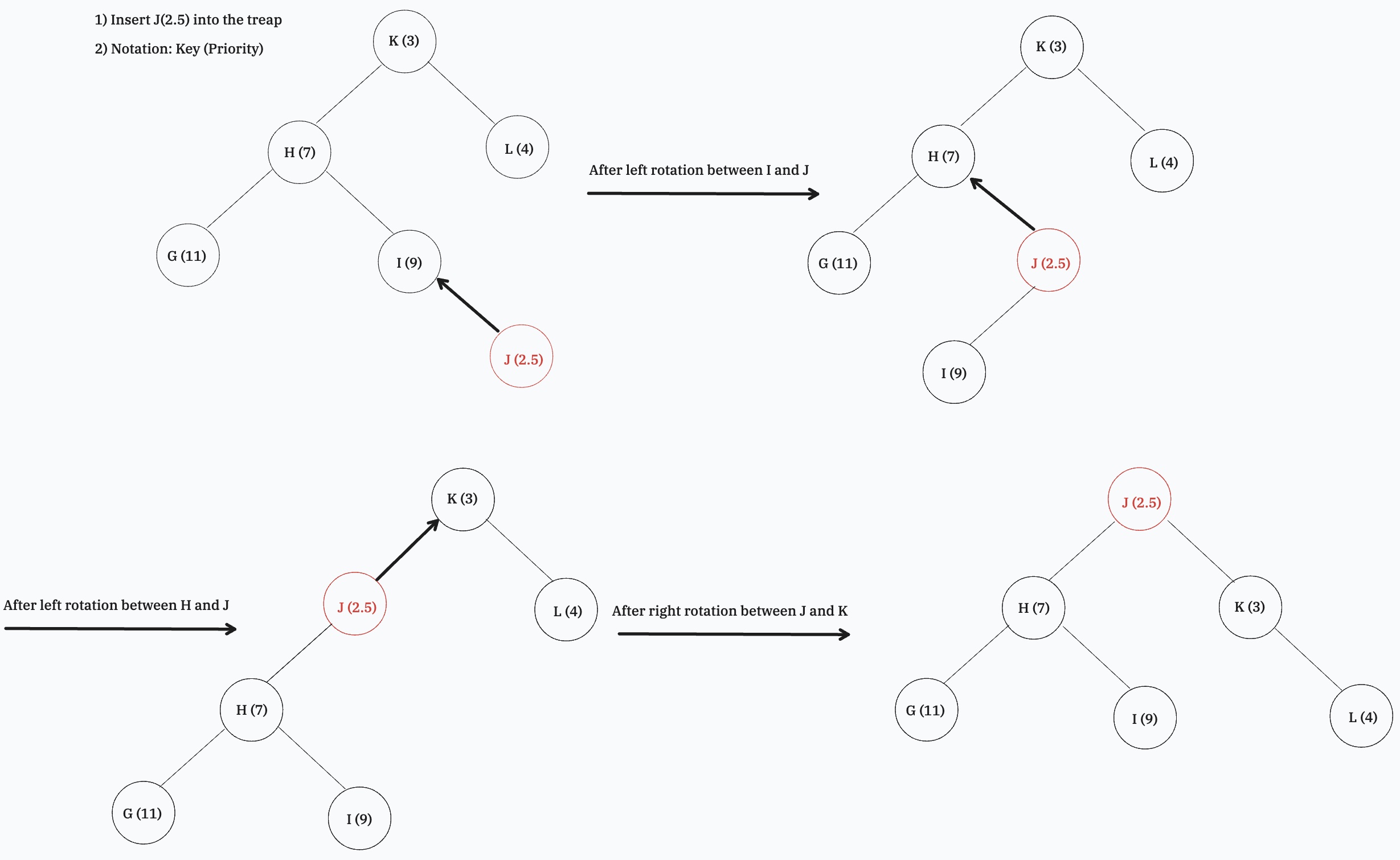
Treap Insertion Example

Implementation of Treap (Golang)

Element

在代码实现中, 我们使用一个 Element class 来存储<key, priority> pairs.

type Element struct {
	id       int64     // unique identifier of an element
	key      int64
	priority int64
}

// create a new element instance
func NewElement(id int64, key int64, priority int64) *Element {
	return &Element{
		id:       id,
		key:      key,
		priority: priority,
	}
}

func (this *Element) GetId() int64 {
	return this.id
}

func (this *Element) GetKey() int64 {
	return this.key
}

func (this *Element) GetPriority() int64 {
	return this.priority
}

// randomly set the priority of an element
func (this *Element) SetRandomPriority() {
	this.priority = rand.Int63n(int64(math.Pow(10, 7)))
}

TreapNode

type TreapNode struct {
	element *Element
	left    *TreapNode   // left child of the treap node
	right   *TreapNode   // right child of the treap node
}

func NewTreapNode(element *Element) *TreapNode {
	return &TreapNode{
		element: element,
		left:    nil,
		right:   nil,
	}
}

Rotation

func rightRotation(parent *TreapNode) *TreapNode {
	leftChild, tempNode := parent.left, parent.left.right
	leftChild.right = parent
	parent.left = tempNode

	return leftChild
}

func leftRotation(parent *TreapNode) *TreapNode {
	rightChild, tempNode := parent.right, parent.right.left
	rightChild.left = parent
	parent.right = tempNode

	return rightChild
}

Insertion

当你成功插入一个新的节点的时候, 新的节点一定是叶子节点 (BST property), 这个时候你就要比较你与你父母节点的 priority, 当你的 priority 比你父母节点的 priority 要小的时候, rotate 直到树中所有的节点都遵循 Min-Heap 性质.

// recursive implementation of insert
func Insert(root *TreapNode, element *Element) *TreapNode {
	if root == nil { // reach the bottom of treap, return with a new node
		return NewTreapNode(element)
	}

	if element.GetKey() <= root.element.GetKey() { // go to the left subtree
		root.left = Insert(root.left, element)
    
		if root.left.element.GetPriority() < root.element.GetPriority() { // right rotation
			root = rightRotation(root)
		}
	} else { // go to the right subtree
		root.right = Insert(root.right, element)
		
		if root.right.element.GetPriority() < root.element.GetPriority() { // left rotation
			root = leftRotation(root)
		}
	}
	return root
}

Search

// recursive implementation of search
func Search(root *TreapNode, key int64) (*TreapNode, int) {
    // return whern you reach null node or when you find the key
	if root == nil || key == root.element.GetKey() {
		return root
	}

	if key < root.element.GetKey() {
		return Search(root.left, key)
	}

	return Search(root.right, key)
}

Delete

当你找到目标节点并进行删除的时候, 你需要考虑以下情况

• 目标节点没有孩子 (也就是叶子结点), 直接将目标节点指向nil
• 目标节点只有左孩子或者右孩子, 直接让左孩子或者右孩子取代目标节点
• 目标节点既有左孩子也有右孩子, 与 priority 更小的孩子进行 rotate. 直到目标节点成为叶子节点才能进行删除

// delete an arbitrary element (if exists) from the treap with a given search key
// return the root node
func Delete(root *TreapNode, key int64) *TreapNode {
	if root == nil {
		return nil
	}

	if key < root.element.GetKey() {
		root.left = Delete(root.left, key)
	} else if key > root.element.GetKey() {
		root.right = Delete(root.right, key)
	} else { // find the key

		if root.left == nil { // the deleted node only has right child
			root = root.right
		} else if root.right == nil { // the deleted only has left child
			root = root.left
		} else if root.left == nil && root.right == nil { // deleted node is a leaf node
			root = nil
		} else { // deleted node has both left and right child
			// push up the node with smaller priority
			// and keep track of the deleted node until it becomes the leaf node
			if root.left.element.GetPriority() < root.right.element.GetPriority() {
				root = rightRotation(root)
				root.right = Delete(root.right, key)
			} else {
				root = leftRotation(root)
				root.left = Delete(root.left, key)
			}
		}
	}
	return root
}

Complexity of Treap Operations

• Expected cost of Insertion: \(O(height) = O(\log n)\)
• Expected cost of Deletion: \(O(\log n)\)
• Expected cost of Search: \(O(\log n)\)